어떤 함수의 기울기를 얘기할 때
대상이 되는 함수는 보통 여러 개의 특성을 갖고 있을 것이다. 즉 다변수 함수다.
따라서 어떤 함수의 기울기는 벡터다. 각각의 특성에 대한 기울기를 한 번에 나타내는 좋은 표기법이기 때문이다.
즉 기울기는 모든 독립 변수에 대한 편미분의 벡터라고 할 수 있으며 다음과 같이 표기한다.

어떤 함수가 다음과 같고, 그 기울기도 다음과 같이 주어져 있다고 해보자.
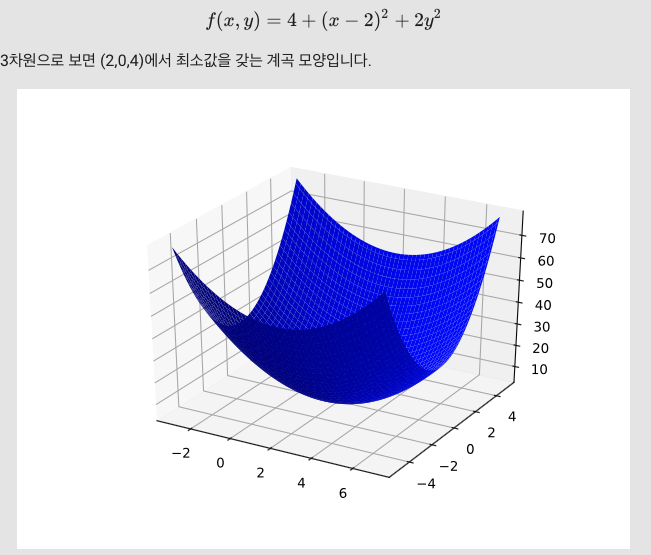
위 함수가 손실 함수라고 할 때, 손실을 줄이는 방향으로 기울기값이 감소하려면 어떤 (x,y)의 방향으로 이동해야 할까? 미분을 해야 알 수 있다. 미분은 방향성과 크기를 알려주는 좋은 척도이기 때문이다. 이 기울기를 이용하여 손실을 줄여나가는 방법이 경사하강법(Gradient Descent)이다.
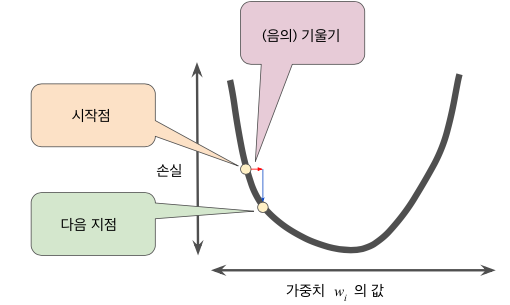
기울기는 벡터다. 벡터는 크기와 방향을 갖는다. 기울기는 항상 손실 함수 값이 증가하는 방향을 향한다. 따라서 기울기의 방향의 반대 방향을 향하게 하여 손실을 줄이는 방향을 향하게 해야 한다. 그리고 보폭의 크기에 해당 기울기를 적용하여(곱하여) 다음 지점을 결정하는 것을 반복함으로써 손실 함수를 감소시키는 방향으로 나아간다.
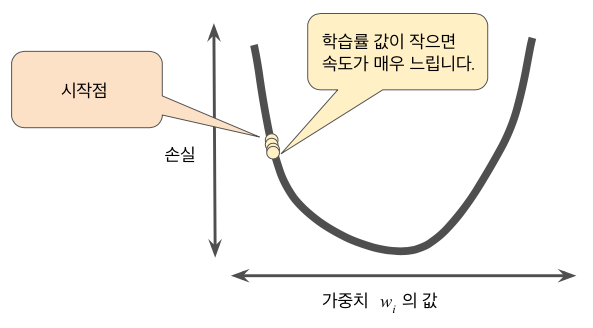
예를 들어 기울기가 2.5이고 학습률이 0.01이면 경사하강법 알고리즘은 이전 지점으로부터 0.025 떨어진 지점을 다음 지점으로 결정한다. 대부분의 머신러닝 프로그래머는 학습률을 미세 조정하는 데 상당한 시간을 소비한다. 학습률을 너무 작게 설정하면 학습 시간이 매우 오래 걸릴 것이다.
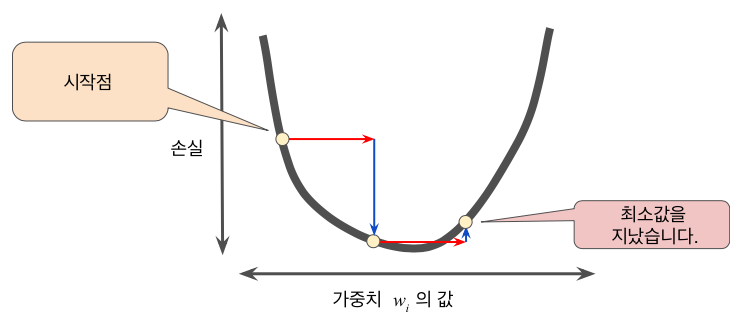
반대로 학습률을 너무 크게 설정하면 곡선의 최저점을 무질서하게 이탈할 우려가 있다.
'Artificial Intelligence > Machine Learning' 카테고리의 다른 글
| 경사하강법(Gradient Descent) (0) | 2018.12.23 |
|---|---|
| 손실(Loss) (0) | 2018.12.23 |
| 머신러닝을 위한 수학 (0) | 2018.12.23 |
| 머신러닝 알고리즘 cheet sheet (0) | 2018.12.23 |
| 머신러닝과 딥러닝의 주요한 차이 (0) | 2018.12.23 |